Page 12 - InsuranceJournal135

วิชาการ IPRB

จากข้อมูลดังกล่าว ส�านักงานฯ จึงเลือกใช้ข้อมูลตั้งแต่ปี 2557 ในการสร้างสมการถดถอย เพื่อสะท้อนถึงสภาวะการแข่งขันในตลาด
ี
ี
ี
และหลีกเล่ยงแนวโน้มท่ผิดปกติจากนโยบายรถยนต์คันแรก โดยการสร้างสมการถดถอยจากข้อมูล อัตราส่วนระหว่างเบ้ยประกันภัยรับตรงต่อ
GDP ที่ขจัดอิทธิพลจากฤดูกาลแล้ว (Y/S) ระหว่างปี 2557 – 2559 โดยสามารถสร้างสมการถดถอยได้ดังสมการที่ 3
t t
สมการที่ (3) : T = ß + ß * lag number
t 0 1
T = 20.062 – 0.078 * lag number
t
เมื่อ T คือ ค่าของอิทธิพลแนวโน้มที่ไตรมาสที่ t
t
ึ
ß คือ สัมประสิทธ์ท่ได้จากสมการถดถอย ซ่งเป็นค่าเฉล่ยของค่าอิทธิพลแนวโน้มเม่อตัวแปรอิสระมีค่าเท่ากับ 0
ี
ี
ื
ิ
0
ี
ึ
ื
ิ
ี
ß คอ สัมประสิทธ์ท่ได้จากสมการถดถอย ซ่งเป็นพารามิเตอร์ท่บอกให้ทราบถึงอัตราการเปล่ยนแปลงของค่า
ี
1
อิทธิพลแนวโน้มเมื่อตัวแปรอิสระ (lag number) มีค่าเพิ่มขึ้น 1 หน่วย
lag number คือ ค่าล�าดับของไตรมาสในชุดข้อมูล
ตารางที่ 3 : ค่าพยากรณ์ค่าอิทธิพลจากแนวโน้มที่ได้จากสมการถดถอย (T ) ส�าหรับแต่ละไตรมาส
t
ปี ไตรมาส 2557 2558 2559 2560*
1 15.63 15.32 15.01 14.70
2 15.55 15.24 14.93 14.62
ค่าอิทธิพลจากแนวโน้ม (T)
t 3 15.48 15.17 14.86 14.54
4 15.40 15.09 14.78 14.47
*ค่าพยากรณ์ที่ได้จากสมการถดถอยดังสมการที่ 3

หลังจากที่ได้ประมาณค่าอิทธิพลจากฤดูกาล (S) และค่าอิทธิพลจากแนวโน้ม (T) ดังที่ได้กล่าวไปแล้ว ส�านักงานฯสามารถพยากรณ์
t t
อัตราส่วนเบี้ยประกันภัยรับตรงต่อ GDP ได้โดยการน�า ค่าอิทธิพลจากแนวโน้ม (T) มาคูณกับ ค่าอิทธิพลจากฤดูกาล (S) ดังสมการที่ 1 และน�า
t t
ี
ี
�
อัตราส่วนเบ้ยประกันภัยรับตรงต่อ GDP ท่ได้จากการพยากรณ์ด้วยสมการท่ 1 มาคูณด้วยค่า GDP ท่ได้จากการประมาณการของสานักงาน
ี
ี
คณะกรรมการพัฒนาการเศรษฐกิจและสังคมแห่งชาติ (NESDB) และคูณด้วย 1,000 บาท ดังสมการท่ 4 โดยจะได้ผลลัพธ์เป็นค่าพยากรณ์
ี
เบี้ยประกันภัยรับตรงดังรูปที่ 4
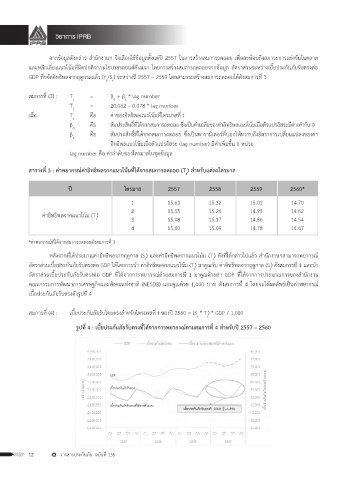
สมการที่ (4) : เบี้ยประกันภัยรับโดยตรงส�าหรับไตรมาสที่ t ของปี 2560 = (S * T) * GDP / 1,000
t t
รูปที่ 4 : เบี้ยประกันภัยรับตรงที่ได้จากการพยากรณ์ตามสมการที่ 4 ส�าหรับปี 2557 – 2560

GDP

เบี้ยประกันภัยรับตรง

เบี้ยประกันภัยรับตรงที่ได้จากตัวแบบ

12 วารสารประกันภัย ฉบับที่ 135